Section 4.1 — Simple linear regression¶
This notebook contains the code examples from Section 4.1 Simple linear regression from the No Bullshit Guide to Statistics.
Notebook setup¶
# load Python modules
import os
import numpy as np
import pandas as pd
import seaborn as sns
import matplotlib.pyplot as plt
# Figures setup
plt.clf() # needed otherwise `sns.set_theme` doesn"t work
from plot_helpers import RCPARAMS
RCPARAMS.update({"figure.figsize": (5, 3)}) # good for screen
# RCPARAMS.update({"figure.figsize": (5, 1.6)}) # good for print
sns.set_theme(
context="paper",
style="whitegrid",
palette="colorblind",
rc=RCPARAMS,
)
# High-resolution please
%config InlineBackend.figure_format = "retina"
# Where to store figures
DESTDIR = "figures/lm/simple"
<Figure size 640x480 with 0 Axes>
from ministats.plots.figures import plot_residuals
from ministats.plots.figures import plot_residuals2
# set random seed for repeatability
np.random.seed(42)
import warnings
# silence kurtosistest warning when using n < 20
warnings.filterwarnings("ignore", category=UserWarning)
$\def\stderr#1{\mathbf{se}_{#1}}$ $\def\stderrhat#1{\hat{\mathbf{se}}_{#1}}$ $\newcommand{\Mean}{\textbf{Mean}}$ $\newcommand{\Var}{\textbf{Var}}$ $\newcommand{\Std}{\textbf{Std}}$ $\newcommand{\Freq}{\textbf{Freq}}$ $\newcommand{\RelFreq}{\textbf{RelFreq}}$ $\newcommand{\DMeans}{\textbf{DMeans}}$ $\newcommand{\Prop}{\textbf{Prop}}$ $\newcommand{\DProps}{\textbf{DProps}}$
$$ \newcommand{\CI}[1]{\textbf{CI}_{#1}} \newcommand{\CIL}[1]{\textbf{L}_{#1}} \newcommand{\CIU}[1]{\textbf{U}_{#1}} \newcommand{\ci}[1]{\textbf{ci}_{#1}} \newcommand{\cil}[1]{\textbf{l}_{#1}} \newcommand{\ciu}[1]{\textbf{u}_{#1}} $$
(this cell contains the macro definitions like $\stderr{\overline{\mathbf{x}}}$, $\stderrhat{}$, $\Mean$, ...)
Definitions¶
Linear model¶
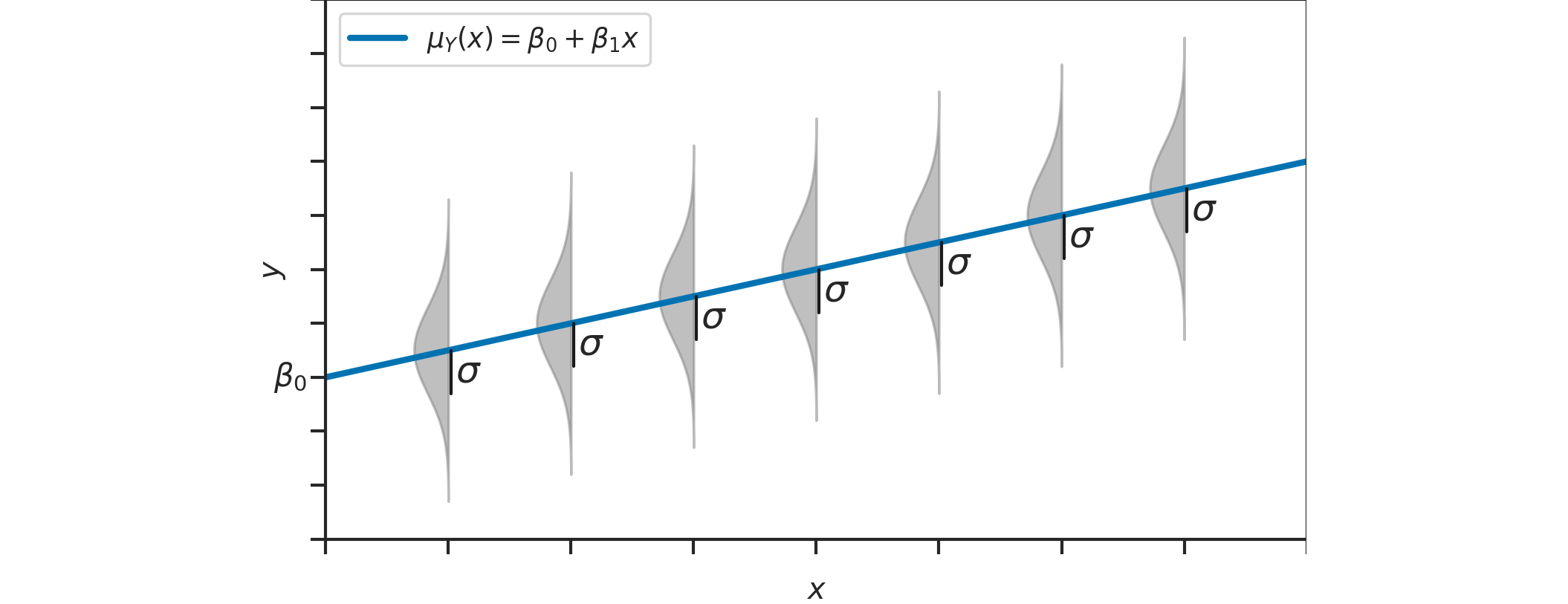
Example: students score as a function of effort¶
students = pd.read_csv("../datasets/students.csv")
students.head()
| student_ID | background | curriculum | effort | score | |
|---|---|---|---|---|---|
| 0 | 1 | arts | debate | 10.96 | 75.0 |
| 1 | 2 | science | lecture | 8.69 | 75.0 |
| 2 | 3 | arts | debate | 8.60 | 67.0 |
| 3 | 4 | arts | lecture | 7.92 | 70.3 |
| 4 | 5 | science | debate | 9.90 | 76.1 |
efforts = students["effort"]
scores = students["score"]
sns.scatterplot(x=efforts, y=scores);
Compute the correlation¶
np.corrcoef(efforts, scores)[0,1]
# ALT. students[["effort","score"]].corr()
# np.corrcoef
0.8794375135614695
Parameter estimation using least squares¶
meaneffort = efforts.mean()
meanscore = scores.mean()
num = np.sum( (efforts-meaneffort)*(scores-meanscore) )
denom = np.sum( (efforts - meaneffort)**2 )
b1 = num / denom
b1
4.504850344209071
b0 = meanscore - b1*meaneffort
b0
32.46580930159963
es = np.linspace(5, 12)
scorehats = b0 + b1*es
sns.lineplot(x=es, y=scorehats)
sns.scatterplot(x=efforts, y=scores);
# # ALT.
# sns.regplot(x=efforts, y=scores, ci=None);
Least squares optimization for the parameters¶
How do we find the parameter estimates of the model?
plot_residuals(efforts, scores, b0, b1)
sns.scatterplot(x=efforts, y=scores)
es = np.linspace(5, 12.2)
scorehats = b0 + b1*es
sns.lineplot(x=es, y=scorehats, color="C4");
ax = sns.scatterplot(x=efforts, y=scores, zorder=4)
es = np.linspace(5, 12.2)
scorehats = b0 + b1*es
sns.lineplot(x=es, y=scorehats, color="C4", zorder=5)
plot_residuals2(efforts, scores, b0, b1, ax=ax);
Estimating the standard deviation parameter¶
scorehats = b0 + b1*efforts
residuals = scores - scorehats
residuals[0:4]
0 -6.838969 1 3.387041 2 -4.207522 3 2.155776 dtype: float64
SSR = np.sum( residuals**2 )
n = len(students)
sigmahat = np.sqrt( SSR / (n-2) )
sigmahat
4.929598282660258
Model diagnostics¶
Scatter plots¶
sns.scatterplot(x="effort", y="score", data=students);
Examples of nonlinear patterns¶
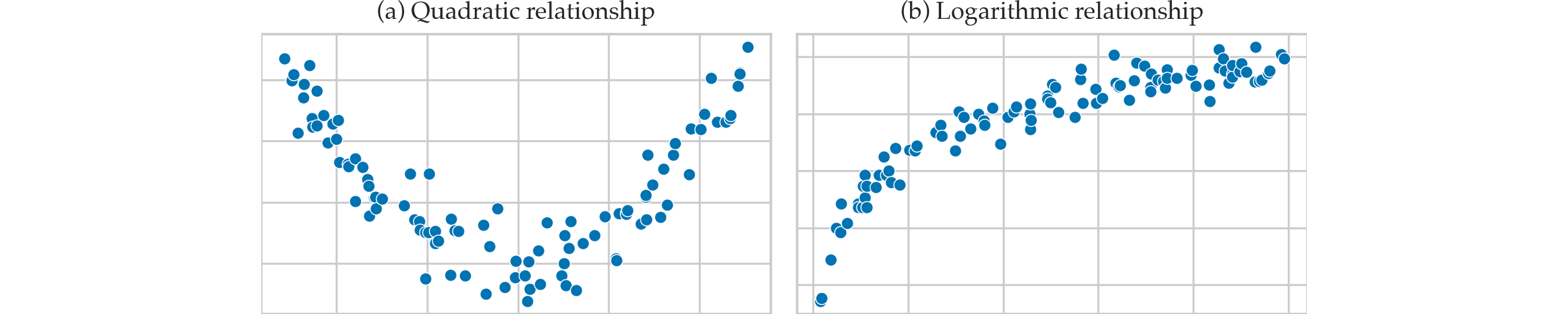
Residuals plots¶
scorehats = b0 + b1*efforts
residuals = scores - scorehats
Residuals versus the predicted values¶
ax = sns.scatterplot(x=scorehats, y=residuals)
ax.set_xlabel("model predictions ($\\hat{s}_i$)")
ax.set_ylabel("residuals ($r_i = s_i - \\hat{s}_i$)")
ax.axhline(y=0, color="b", linestyle="dotted");
Residuals versus the predictor (bonus)¶
# ax = sns.scatterplot(x=efforts, y=residuals)
# ax.set_xticks(range(5,12+1))
# ax.set_ylabel("residuals ($r_i = s_i - \\hat{s}_i$)")
# ax.axhline(y=0, color="b", linestyle="dotted");
QQ-plot of the residuals¶
from statsmodels.graphics.api import qqplot
qqplot(residuals, line="s");
Residual plots that show violated assumptions¶
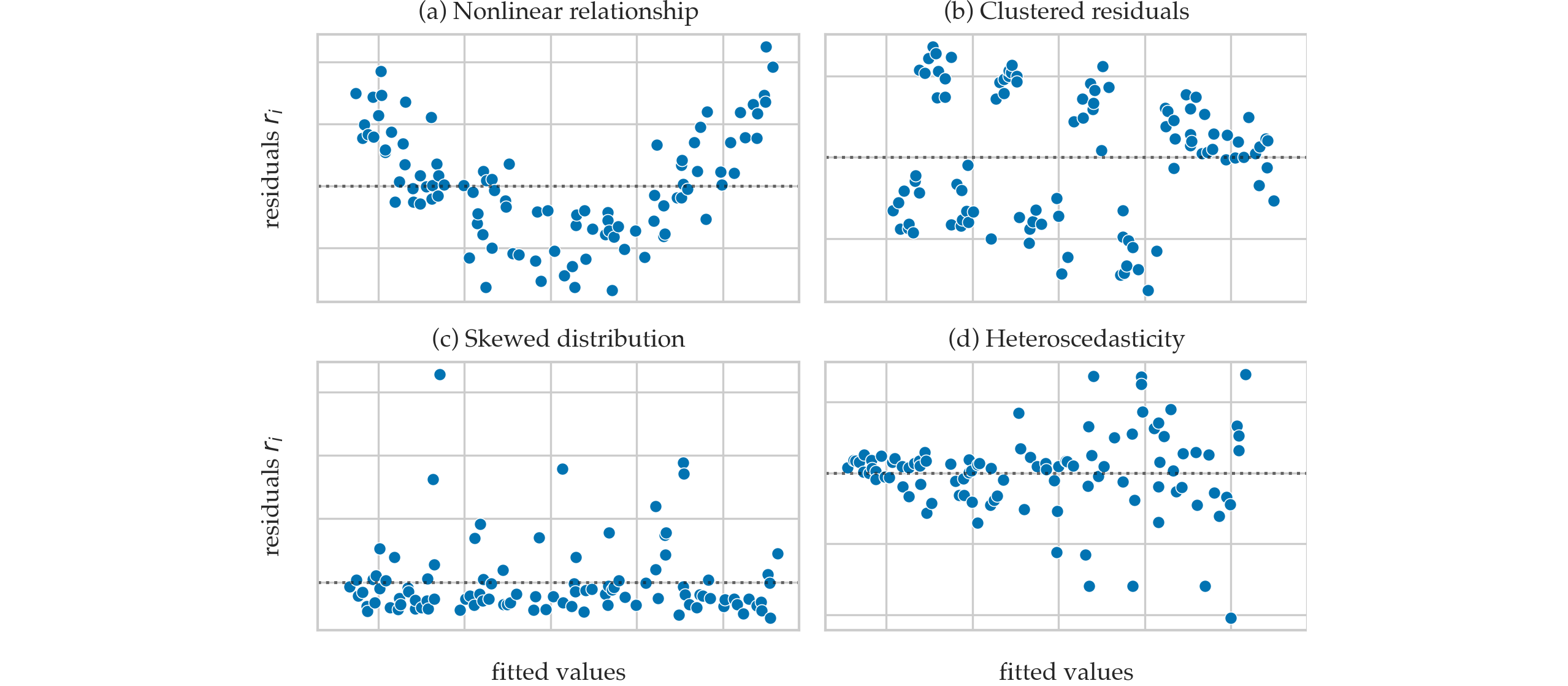
Sum of squares quantities¶
Sum of squared residuals¶
SSR = np.sum( residuals**2 )
SSR
315.9122099692906
Explained sum of squares¶
meanscore = scores.mean()
ESS = np.sum( (scorehats-meanscore)**2 )
ESS
1078.2917900307098
Total sum of squares¶
TSS = np.sum( (scores - meanscore)**2 )
TSS
1394.2040000000002
SSR + ESS # == TSS
1394.2040000000004
Coefficient of determination $R^2$¶
R2 = ESS / TSS
R2
0.7734103402591799
Using linear models to make predictions¶
def predict(x, b0, b1):
yhat = b0 + b1*x
return yhat
Confidence interval for the mean¶
TODO: add formulas
Confidence interval for observations¶
TODO: add formulas
Example:predicting students' scores¶
Predict the score of a new student who invests 9 hours of effort per week.
neweffort = 9
scorehat = predict(neweffort, b0=32.5, b1=4.5)
scorehat
73.0
Confidence interval for the mean score¶
#######################################################
newdev = (neweffort - efforts.mean())**2
sum_dev2 = np.sum((efforts - efforts.mean())**2)
se_meanscore = sigmahat*np.sqrt(1/n + newdev/sum_dev2)
se_meanscore
1.2744485881877106
from scipy.stats import t as tdist
alpha = 0.1
t_l, t_u = tdist(df=n-2).ppf([alpha/2, 1-alpha/2])
[scorehat + t_l*se_meanscore, scorehat + t_u*se_meanscore]
[70.74303643371016, 75.25696356628984]
Prediction band for the mean score¶
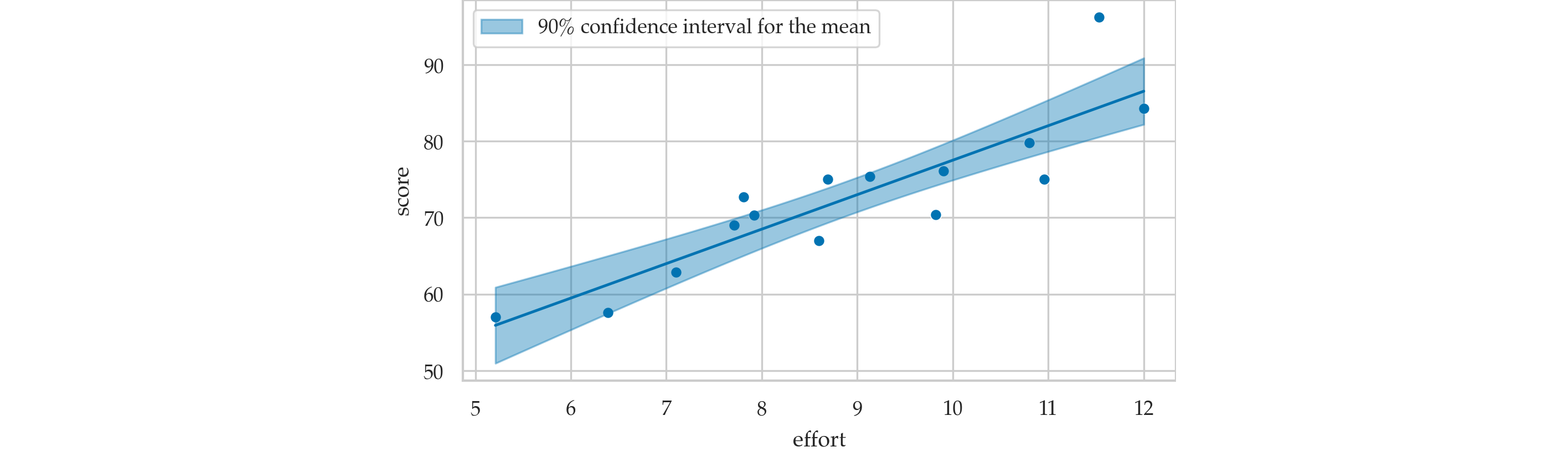
Confidence interval for predicted scores¶
se_score = sigmahat*np.sqrt(1 + 1/n + newdev/sum_dev2)
se_score
5.0916754052414435
alpha = 0.1
t_l, t_u = tdist(df=n-2).ppf([alpha/2, 1-alpha/2])
[scorehat + t_l*se_score, scorehat + t_u*se_score]
[63.98298198333331, 82.0170180166667]
Prediction band for scores¶
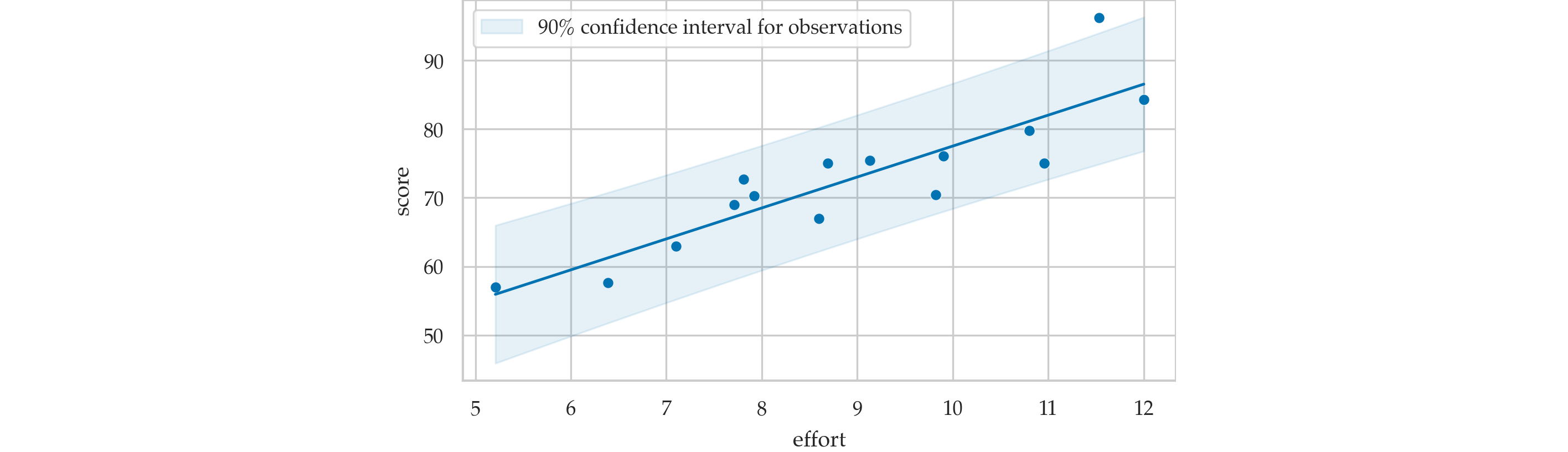
Prediction caveats¶
efforts.min(), efforts.max()
(5.21, 12.0)
It's not OK to extrapolate the validity of the model outside of the range of values where we have observed data.
For example, there is no reason to believe in the model's predictions about an effort of 20 hours per week:
predict(20, b0=32.5, b1=4.5)
122.5
Indeed, the model predicts the grade will be above 100% which is impossible.
Explanations¶
Software for fitting linear models¶
scipystatsmodelsscikit-learn
Fitting linear models with statsmodels¶
import statsmodels.formula.api as smf
lm1 = smf.ols("score ~ 1 + effort", data=students).fit()
type(lm1)
statsmodels.regression.linear_model.RegressionResultsWrapper
Estimated parameters for the model¶
lm1.params
Intercept 32.465809 effort 4.504850 dtype: float64
type(lm1.params)
pandas.core.series.Series
We often want to extract the intercept and slope parameters for use in subsequent calculations.
b0 = lm1.params["Intercept"] # = lm1.params[0]
b1 = lm1.params["effort"] # = lm1.params[1]
b0, b1
(32.465809301599606, 4.504850344209074)
The estimate $\widehat{\sigma}$ is obtained by taking the square root of the .scale attribute.
sigmahat = np.sqrt(lm1.scale)
sigmahat
4.929598282660258
Model fitted values¶
lm1.fittedvalues # == scorehats
0 81.838969 1 71.612959 2 71.207522 3 68.144224 4 77.063828 5 81.118193 6 67.648690 7 73.595093 8 55.936080 9 67.198205 10 76.703440 11 84.406734 12 64.450247 13 61.251803 14 86.524013 dtype: float64
Residuals¶
lm1.resid # == scores - scorehats
0 -6.838969 1 3.387041 2 -4.207522 3 2.155776 4 -0.963828 5 -1.318193 6 5.051310 7 1.804907 8 1.063920 9 1.801795 10 -6.303440 11 11.793266 12 -1.550247 13 -3.651803 14 -2.224013 dtype: float64
Sum-of-squared quantities¶
# SSR # ESS # TSS # R2
lm1.ssr, lm1.ess, lm1.centered_tss, lm1.rsquared
(315.91220996929053, 1078.2917900307098, 1394.2040000000002, 0.7734103402591798)
Predictions¶
Predict the score of a new student who invests 9 hours of effort per week.
lm1.predict({"effort":9})
0 73.009462 dtype: float64
pred = lm1.get_prediction({"effort":9})
pred.se_mean, pred.conf_int(alpha=0.1)
(array([1.27444859]), array([[70.75249883, 75.26642597]]))
pred.se_obs, pred.conf_int(obs=True, alpha=0.1)
(array([5.09167541]), array([[63.99244438, 82.02648042]]))
Model summary table¶
lm1.summary()
| Dep. Variable: | score | R-squared: | 0.773 |
|---|---|---|---|
| Model: | OLS | Adj. R-squared: | 0.756 |
| Method: | Least Squares | F-statistic: | 44.37 |
| Date: | Thu, 18 Jul 2024 | Prob (F-statistic): | 1.56e-05 |
| Time: | 11:53:14 | Log-Likelihood: | -44.140 |
| No. Observations: | 15 | AIC: | 92.28 |
| Df Residuals: | 13 | BIC: | 93.70 |
| Df Model: | 1 | ||
| Covariance Type: | nonrobust |
| coef | std err | t | P>|t| | [0.025 | 0.975] | |
|---|---|---|---|---|---|---|
| Intercept | 32.4658 | 6.155 | 5.275 | 0.000 | 19.169 | 45.763 |
| effort | 4.5049 | 0.676 | 6.661 | 0.000 | 3.044 | 5.966 |
| Omnibus: | 4.062 | Durbin-Watson: | 2.667 |
|---|---|---|---|
| Prob(Omnibus): | 0.131 | Jarque-Bera (JB): | 1.777 |
| Skew: | 0.772 | Prob(JB): | 0.411 |
| Kurtosis: | 3.677 | Cond. No. | 44.5 |
Notes:
[1] Standard Errors assume that the covariance matrix of the errors is correctly specified.
Helper functions for plotting linear model results¶
plot_reg(lm): generate a regression plot for the modellmplot_redid(lm): residuals plot for the modellmplot_pred_bands(lm, ...): plot confidence intervals modellm. Useci_mean=Trueto plot the predictions for the mean, orci_obs=Trueto plot the predictions of the observations variable.
Regression plot¶
from ministats import plot_reg
plot_reg(lm1);
Residuals plot¶
xs = np.array([1,2,3])
hasattr(xs, "name")
False
xs = pd.Series([1,2,3])
hasattr(xs, "name") and xs.name is not None
False
from ministats import plot_resid
plot_resid(lm1);
# BONUS plot residuals against predictor variable
plot_resid(lm1, pred="effort");
Prediction band plots¶
from ministats import plot_pred_bands
plot_reg(lm1)
plot_pred_bands(lm1, ci_mean=True, alpha_mean=0.1);
plot_reg(lm1)
plot_pred_bands(lm1, ci_obs=True, alpha_obs=0.1);
Seaborn functions for plotting linear models¶
Regression plot¶
sns.regplot(x="effort", y="score", ci=None, data=students);
Residual plot¶
sns.residplot(x="effort", y="score", data=students);
Pearson correlation coefficient revisited¶
Related to the Pearson correlation coefficient¶
efforts = students["effort"]
scores = students["score"]
pearson_r = efforts.corr(scores)
pearson_r
0.8794375135614695
# # ALT.
# from scipy.stats import pearsonr
# pearson_r = pearsonr(efforts, scores)[0]
pearson_r**2
0.7734103402591799
lm1 = smf.ols("score ~ 1 + effort", data=students).fit()
lm1.rsquared
0.7734103402591798
Alternative methods for fitting linear models (optional)¶
Numerical optimization¶
from scipy.optimize import minimize
def ssr(betas, xdata, ydata):
yhat = betas[0] + betas[1]*xdata
resid = ydata - yhat
return np.sum(resid**2)
optres = minimize(ssr, x0=[0,0], args=(efforts,scores))
beta0, beta1 = optres.x
beta0, beta1
(32.465809793102544, 4.504850301246796)
Linear algebra¶
linear algebra solution using numpy
import numpy as np
# Prepare the design matrix
n = len(students)
X = np.ndarray((n,2))
X[:,0] = 1
X[:,1] = efforts
X
array([[ 1. , 10.96],
[ 1. , 8.69],
[ 1. , 8.6 ],
[ 1. , 7.92],
[ 1. , 9.9 ],
[ 1. , 10.8 ],
[ 1. , 7.81],
[ 1. , 9.13],
[ 1. , 5.21],
[ 1. , 7.71],
[ 1. , 9.82],
[ 1. , 11.53],
[ 1. , 7.1 ],
[ 1. , 6.39],
[ 1. , 12. ]])
We obtain the least squares solution using the Moore–Penrose inverse formula:
$$ \vec{\beta} = (X^{\sf T} X)^{-1}X^{\sf T}\; \mathbf{y} $$
lares = np.linalg.inv(X.T.dot(X)).dot(X.T).dot(scores)
beta0, beta1 = lares
beta0, beta1
(32.46580930159923, 4.504850344209087)
Fitting linear models using scipy¶
The helper function scipy.stats.linregress ...
from scipy.stats import linregress
scipyres = linregress(efforts, scores)
scipyres.intercept, scipyres.slope
(32.46580930159963, 4.504850344209071)
Fitting linear models using scikit-learn¶
The class sklearn.linear_model.LinearRegression ...
from sklearn.linear_model import LinearRegression
sklmodel = LinearRegression()
sklmodel.fit(efforts.values[:,np.newaxis], scores)
sklmodel.intercept_, sklmodel.coef_
(32.46580930159961, array([4.50485034]))
Using the low-level statsmodels API¶
import statsmodels.api as sm
X = sm.add_constant(efforts)
y = scores
smres = sm.OLS(y,X).fit()
smres.params["const"], smres.params["effort"]
(32.465809301599606, 4.504850344209074)
Discussion¶
Examples of non-linear relationships¶
Hare are some examples of the different possible relationships between the effort and score variables.
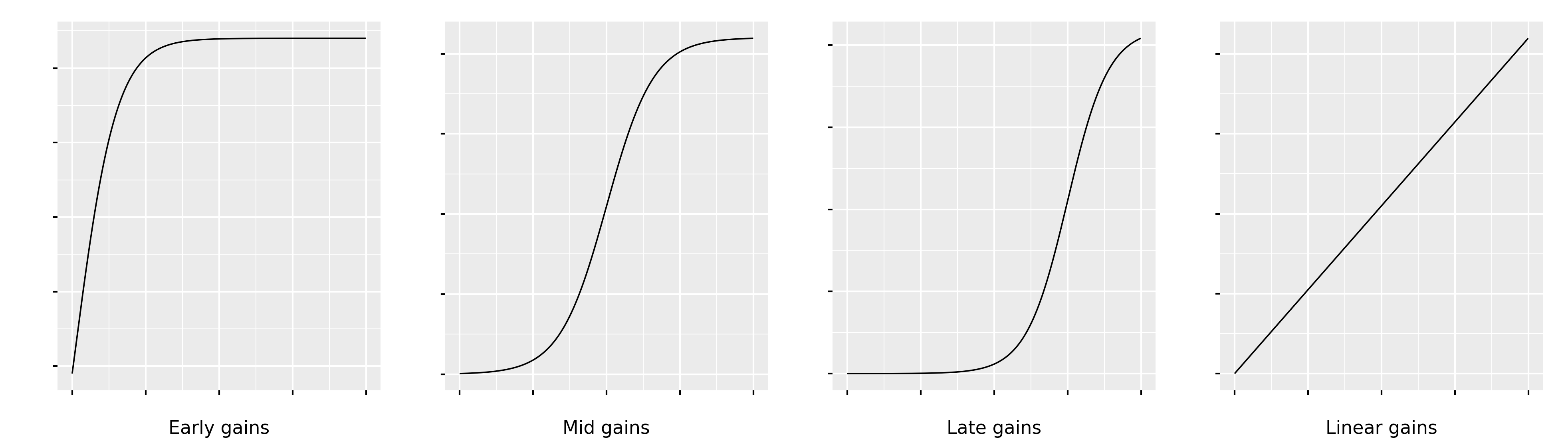
Exercises¶
Exercise E??: marketing dataset¶
marketing = pd.read_csv("../datasets/exercises/marketing.csv")
print(marketing.columns)
lm_mkt = smf.ols("sales ~ 1 + youtube", data=marketing).fit()
plot_reg(lm_mkt)
Index(['youtube', 'facebook', 'newspaper', 'sales'], dtype='object')
<Axes: xlabel='youtube', ylabel='sales'>
from ministats import plot_resid
plot_resid(lm_mkt)
<Axes: xlabel='fitted values', ylabel='residuals $r_i$'>
Links¶
(BONUS MATERIAL) Formula for standard error of coefficients¶
lm1.bse
Intercept 6.155051 effort 0.676276 dtype: float64
Formula using summations
$$ se(\beta_0) = \hat{\sigma} \cdot \sqrt{ \frac{1}{n} + \frac{\overline{x}^2}{\sum (x_i - \overline{x})^2} } \qquad se(\beta_1) = \hat{\sigma} \cdot \sqrt{\frac{1}{\sum (x_i - \overline{x})^2}} $$
TODO: show derivation why these formulas are equiv. to matrix formulas below when p=1
sum_dev2 = np.sum((efforts - efforts.mean())**2)
se_Intercept = sigmahat * np.sqrt(1/n + efforts.mean()**2/sum_dev2)
se_b_effort = sigmahat/np.sqrt(sum_dev2)
se_Intercept, se_b_effort
(6.155051380977695, 0.6762756464968055)
Alternative formula using design matrix
$$ [se(\beta_0), se(\beta_1)] = \hat{\sigma} \cdot \text{diag}\left( \sqrt{ (X^T X)^{-1} } \right) $$
where $X$ is the design matrix.
# construct the design matrix for the model
X = sm.add_constant(students[["effort"]])
# calculate the diagonal of the inverse-covariance matrix
inv_covs = np.diag(np.linalg.inv(X.T.dot(X)))
np.sqrt(sigmahat**2 * inv_covs)
array([6.15505138, 0.67627565])
lm1.model.exog[:,1]
array([10.96, 8.69, 8.6 , 7.92, 9.9 , 10.8 , 7.81, 9.13, 5.21,
7.71, 9.82, 11.53, 7.1 , 6.39, 12. ])