Section 4.4 — Regression with categorical predictors¶

This notebook contains the code examples from Section 4.4 Regression with categorical predictors from the No Bullshit Guide to Statistics.

Notebook setup¶

In [1]:

# load Python modules
import os
import numpy as np
import pandas as pd
import seaborn as sns
import matplotlib.pyplot as plt

# load Python modules import os import numpy as np import pandas as pd import seaborn as sns import matplotlib.pyplot as plt

In [2]:

# Figures setup
plt.clf()  # needed otherwise `sns.set_theme` doesn't work
from plot_helpers import RCPARAMS
# RCPARAMS.update({'figure.figsize': (10, 3)})   # good for screen
RCPARAMS.update({'figure.figsize': (5, 1.6)})    # good for print
sns.set_theme(
    context="paper",
    style="whitegrid",
    palette="colorblind",
    rc=RCPARAMS,
)

# High-resolution please
%config InlineBackend.figure_format = 'retina'

# Where to store figures
DESTDIR = "figures/lm/categorical"

# Figures setup plt.clf() # needed otherwise `sns.set_theme` doesn't work from plot_helpers import RCPARAMS # RCPARAMS.update({'figure.figsize': (10, 3)}) # good for screen RCPARAMS.update({'figure.figsize': (5, 1.6)}) # good for print sns.set_theme( context="paper", style="whitegrid", palette="colorblind", rc=RCPARAMS, ) # High-resolution please %config InlineBackend.figure_format = 'retina' # Where to store figures DESTDIR = "figures/lm/categorical"

<Figure size 640x480 with 0 Axes>

In [3]:

#######################################################

#######################################################

In [ ]:

In [ ]:

Definitions¶

In [4]:

import pandas as pd
import statsmodels.formula.api as smf

import pandas as pd import statsmodels.formula.api as smf

Design matrix for linear model lm1¶

In [5]:

students = pd.read_csv("../datasets/students.csv")
lm1 = smf.ols("score ~ 1 + effort", data=students).fit()
lm1.model.exog[0:3]

students = pd.read_csv("../datasets/students.csv") lm1 = smf.ols("score ~ 1 + effort", data=students).fit() lm1.model.exog[0:3]

Out[5]:

array([[ 1.  , 10.96],
       [ 1.  ,  8.69],
       [ 1.  ,  8.6 ]])

In [6]:

students["effort"].values[0:3]

students["effort"].values[0:3]

Out[6]:

array([10.96,  8.69,  8.6 ])

Design matrix for linear model lm2¶

In [7]:

doctors = pd.read_csv("../datasets/doctors.csv")
formula = "score ~ 1 + alc + weed + exrc"
lm2  = smf.ols(formula, data=doctors).fit()
lm2.model.exog[0:3]

doctors = pd.read_csv("../datasets/doctors.csv") formula = "score ~ 1 + alc + weed + exrc" lm2 = smf.ols(formula, data=doctors).fit() lm2.model.exog[0:3]

Out[7]:

array([[ 1. ,  0. ,  5. ,  0. ],
       [ 1. , 20. ,  0. ,  4.5],
       [ 1. ,  1. ,  0. ,  7. ]])

In [8]:

doctors[["alc","weed","exrc"]].values[0:3]

doctors[["alc","weed","exrc"]].values[0:3]

Out[8]:

array([[ 0. ,  5. ,  0. ],
       [20. ,  0. ,  4.5],
       [ 1. ,  0. ,  7. ]])

Example 1: binary predictor variable¶

In [9]:

import statsmodels.formula.api as smf
lmloc = smf.ols("score ~ 1 + C(loc)", data=doctors).fit()
lmloc.params

import statsmodels.formula.api as smf lmloc = smf.ols("score ~ 1 + C(loc)", data=doctors).fit() lmloc.params

Out[9]:

Intercept        52.956522
C(loc)[T.urb]    -6.992885
dtype: float64

In [10]:

rur_mean = doctors[doctors["loc"]=="rur"]["score"].mean()
urb_mean = doctors[doctors["loc"]=="urb"]["score"].mean()

rur_mean, urb_mean, urb_mean - rur_mean

rur_mean = doctors[doctors["loc"]=="rur"]["score"].mean() urb_mean = doctors[doctors["loc"]=="urb"]["score"].mean() rur_mean, urb_mean, urb_mean - rur_mean

Out[10]:

(52.95652173913044, 45.96363636363636, -6.992885375494076)

Encoding¶

In [11]:

doctors["loc"][0:5]

doctors["loc"][0:5]

Out[11]:

0    rur
1    urb
2    urb
3    urb
4    rur
Name: loc, dtype: object

In [12]:

lmloc.model.exog[0:5]

lmloc.model.exog[0:5]

Out[12]:

array([[1., 0.],
       [1., 1.],
       [1., 1.],
       [1., 1.],
       [1., 0.]])

In [13]:

# ALT.
# dmatrix("1 + C(loc)", doctors)[0:5]

# ALT. # dmatrix("1 + C(loc)", doctors)[0:5]

Dummy coding for categorical predictors¶

In [14]:

cats = ["A", "B", "C", "C"]
catdf = pd.DataFrame({"cat":cats})
catdf

cats = ["A", "B", "C", "C"] catdf = pd.DataFrame({"cat":cats}) catdf

Out[14]:

	cat
0	A
1	B
2	C
3	C

In [15]:

from patsy import dmatrix

dmatrix("1 + C(cat)", data=catdf)

from patsy import dmatrix dmatrix("1 + C(cat)", data=catdf)

Out[15]:

DesignMatrix with shape (4, 3)
  Intercept  C(cat)[T.B]  C(cat)[T.C]
          1            0            0
          1            1            0
          1            0            1
          1            0            1
  Terms:
    'Intercept' (column 0)
    'C(cat)' (columns 1:3)

Example 2: predictors with three levels¶

In [16]:

doctors = pd.read_csv("../datasets/doctors.csv")
doctors["work"].head(5)

doctors = pd.read_csv("../datasets/doctors.csv") doctors["work"].head(5)

Out[16]:

0    hos
1    cli
2    hos
3    eld
4    cli
Name: work, dtype: object

In [17]:

dmatrix("1 + C(work)", data=doctors)[0:5]

dmatrix("1 + C(work)", data=doctors)[0:5]

Out[17]:

array([[1., 0., 1.],
       [1., 0., 0.],
       [1., 0., 1.],
       [1., 1., 0.],
       [1., 0., 0.]])

In [18]:

lmw = smf.ols("score ~ 1 + C(work)", data=doctors).fit()
lmw.params

lmw = smf.ols("score ~ 1 + C(work)", data=doctors).fit() lmw.params

Out[18]:

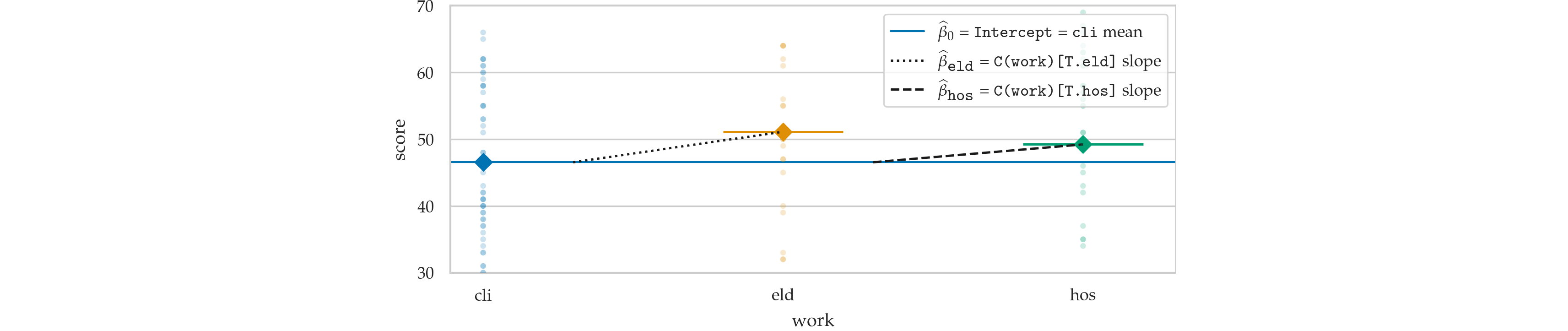
Intercept         46.545455
C(work)[T.eld]     4.569930
C(work)[T.hos]     2.668831
dtype: float64

In [19]:

lmw.rsquared

lmw.rsquared

Out[19]:

0.0077217625749193

In [20]:

lmw.fvalue, lmw.f_pvalue

lmw.fvalue, lmw.f_pvalue

Out[20]:

(0.5953116925291129, 0.5526627461285702)

In [ ]:

Example 3: improved model for the sleep scores¶

We can mix of numerical and categorical predictors

In [21]:

formula3 = "score ~ 1 + alc + weed + exrc + C(loc)"
lm3 = smf.ols(formula3, data=doctors).fit()
lm3.params

formula3 = "score ~ 1 + alc + weed + exrc + C(loc)" lm3 = smf.ols(formula3, data=doctors).fit() lm3.params

Out[21]:

Intercept        63.606961
C(loc)[T.urb]    -5.002404
alc              -1.784915
weed             -0.840668
exrc              1.783107
dtype: float64

In [22]:

lm3.rsquared, lm3.aic

lm3.rsquared, lm3.aic

Out[22]:

(0.8544615790287665, 1092.5985552344712)

In [23]:

from ministats import plot_partreg

plot_partreg(lm3, "alc");

from ministats import plot_partreg plot_partreg(lm3, "alc");

In [24]:

lm3.summary()

lm3.summary()

Out[24]:

OLS Regression Results

Dep. Variable:	score	R-squared:	0.854
Model:	OLS	Adj. R-squared:	0.851
Method:	Least Squares	F-statistic:	221.6
Date:	Fri, 19 Jul 2024	Prob (F-statistic):	4.18e-62
Time:	09:45:06	Log-Likelihood:	-541.30
No. Observations:	156	AIC:	1093.
Df Residuals:	151	BIC:	1108.
Df Model:	4
Covariance Type:	nonrobust

	coef	std err	t	P>|t|	[0.025	0.975]
Intercept	63.6070	1.524	41.734	0.000	60.596	66.618
C(loc)[T.urb]	-5.0024	1.401	-3.572	0.000	-7.770	-2.235
alc	-1.7849	0.068	-26.424	0.000	-1.918	-1.651
weed	-0.8407	0.462	-1.821	0.071	-1.753	0.071
exrc	1.7831	0.133	13.400	0.000	1.520	2.046

Omnibus:	4.325	Durbin-Watson:	1.823
Prob(Omnibus):	0.115	Jarque-Bera (JB):	4.038
Skew:	0.279	Prob(JB):	0.133
Kurtosis:	3.556	Cond. No.	46.2

Notes:
[1] Standard Errors assume that the covariance matrix of the errors is correctly specified.

Compare to the model without loc predictor¶

In [25]:

formula2 = "score ~ 1 + alc + weed + exrc"
lm2 = smf.ols(formula2, data=doctors).fit()
F, p, _ = lm3.compare_f_test(lm2)
F, p

formula2 = "score ~ 1 + alc + weed + exrc" lm2 = smf.ols(formula2, data=doctors).fit() F, p, _ = lm3.compare_f_test(lm2) F, p

Out[25]:

(12.758115596295623, 0.0004759812308491827)

Everything is a linear model¶

One-sample t-test as a linear model¶

In [26]:

kombucha = pd.read_csv("../datasets/kombucha.csv")
ksample04 = kombucha[kombucha["batch"]==4]["volume"]
ksample04.mean()

kombucha = pd.read_csv("../datasets/kombucha.csv") ksample04 = kombucha[kombucha["batch"]==4]["volume"] ksample04.mean()

Out[26]:

1003.8335

In [27]:

from scipy.stats import ttest_1samp
resk = ttest_1samp(ksample04, popmean=1000)
resk.statistic, resk.pvalue

from scipy.stats import ttest_1samp resk = ttest_1samp(ksample04, popmean=1000) resk.statistic, resk.pvalue

Out[27]:

(3.087703149420272, 0.0037056653503329618)

In [28]:

# # ALT. using the helper function from `ministats`
# from ministats import ttest_mean
# ttest_mean(ksample04, mu0=1000)

# # ALT. using the helper function from `ministats` # from ministats import ttest_mean # ttest_mean(ksample04, mu0=1000)

In [29]:

# Prepare zero-centered data (volume - 1000)
kdat04 = pd.DataFrame()
kdat04["zcvolume"] = ksample04 - 1000

# Fit linear model with only an intercept term
import statsmodels.formula.api as smf
lmk = smf.ols("zcvolume ~ 1", data=kdat04).fit()
lmk.params

# Prepare zero-centered data (volume - 1000) kdat04 = pd.DataFrame() kdat04["zcvolume"] = ksample04 - 1000 # Fit linear model with only an intercept term import statsmodels.formula.api as smf lmk = smf.ols("zcvolume ~ 1", data=kdat04).fit() lmk.params

Out[29]:

Intercept    3.8335
dtype: float64

In [30]:

lmk.tvalues.iloc[0], lmk.pvalues.iloc[0]

lmk.tvalues.iloc[0], lmk.pvalues.iloc[0]

Out[30]:

(3.0877031494203044, 0.0037056653503326335)

Two-sample t-test as a linear model¶

East vs. West electricity prices¶

In [31]:

eprices = pd.read_csv("../datasets/eprices.csv")
pricesW = eprices[eprices["loc"]=="West"]["price"]
pricesE = eprices[eprices["loc"]=="East"]["price"]
pricesW.mean() - pricesE.mean()

eprices = pd.read_csv("../datasets/eprices.csv") pricesW = eprices[eprices["loc"]=="West"]["price"] pricesE = eprices[eprices["loc"]=="East"]["price"] pricesW.mean() - pricesE.mean()

Out[31]:

3.000000000000001

Two-sample t-test with pooled variance¶

In [32]:

from scipy.stats import ttest_ind
rese = ttest_ind(pricesW, pricesE, equal_var=True)
rese.statistic, rese.pvalue

from scipy.stats import ttest_ind rese = ttest_ind(pricesW, pricesE, equal_var=True) rese.statistic, rese.pvalue

Out[32]:

(5.022875513276465, 0.00012497067987678488)

In [33]:

ci_Delta = rese.confidence_interval(confidence_level=0.9)
[ci_Delta.low, ci_Delta.high]

ci_Delta = rese.confidence_interval(confidence_level=0.9) [ci_Delta.low, ci_Delta.high]

Out[33]:

[1.957240525873166, 4.042759474126836]

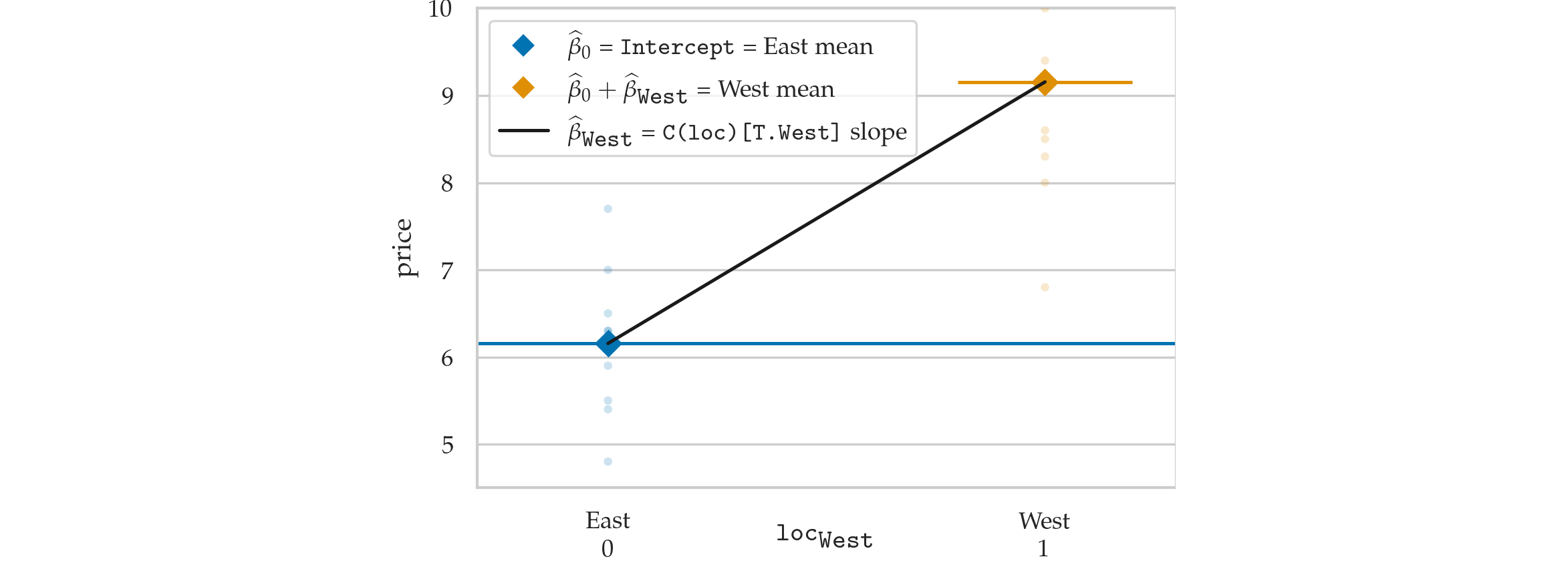
Linear model approach¶

In [34]:

lme = smf.ols("price ~ 1 + C(loc)", data=eprices).fit()
print(lme.params)
lme.tvalues.iloc[1], lme.pvalues.iloc[1]

lme = smf.ols("price ~ 1 + C(loc)", data=eprices).fit() print(lme.params) lme.tvalues.iloc[1], lme.pvalues.iloc[1]

Intercept         6.155556
C(loc)[T.West]    3.000000
dtype: float64

Out[34]:

(5.02287551327646, 0.00012497067987678602)

In [35]:

lme.conf_int(alpha=0.1).iloc[1].values

lme.conf_int(alpha=0.1).iloc[1].values

Out[35]:

array([1.95724053, 4.04275947])

Example 1 (revisited): urban vs. rural doctors¶

In [36]:

from scipy.stats import ttest_ind

scoresR = doctors[doctors["loc"]=="rur"]["score"]
scoresU = doctors[doctors["loc"]=="urb"]["score"]

resloc = ttest_ind(scoresU, scoresR, equal_var=True)
resloc.statistic, resloc.pvalue

from scipy.stats import ttest_ind scoresR = doctors[doctors["loc"]=="rur"]["score"] scoresU = doctors[doctors["loc"]=="urb"]["score"] resloc = ttest_ind(scoresU, scoresR, equal_var=True) resloc.statistic, resloc.pvalue

Out[36]:

(-1.9657612140164198, 0.05112460353979369)

In [37]:

lmloc = smf.ols("score ~ 1 + C(loc)", data=doctors).fit()
lmloc.tvalues.iloc[1], lmloc.pvalues.iloc[1]

lmloc = smf.ols("score ~ 1 + C(loc)", data=doctors).fit() lmloc.tvalues.iloc[1], lmloc.pvalues.iloc[1]

Out[37]:

(-1.9657612140164218, 0.051124603539793465)

In [ ]:

One-way ANOVA as a linear model¶

In [38]:

from scipy.stats import f_oneway

scoresH = doctors[doctors["work"]=="hos"]["score"]
scoresC = doctors[doctors["work"]=="cli"]["score"]
scoresE = doctors[doctors["work"]=="eld"]["score"]

resw = f_oneway(scoresH, scoresC, scoresE)
resw.statistic, resw.pvalue

from scipy.stats import f_oneway scoresH = doctors[doctors["work"]=="hos"]["score"] scoresC = doctors[doctors["work"]=="cli"]["score"] scoresE = doctors[doctors["work"]=="eld"]["score"] resw = f_oneway(scoresH, scoresC, scoresE) resw.statistic, resw.pvalue

Out[38]:

(0.5953116925291182, 0.5526627461285608)

In [39]:

lmw = smf.ols("score ~ 1 + C(work)", data=doctors).fit()
print(lmw.params)
lmw.fvalue, lmw.f_pvalue

lmw = smf.ols("score ~ 1 + C(work)", data=doctors).fit() print(lmw.params) lmw.fvalue, lmw.f_pvalue

Intercept         46.545455
C(work)[T.eld]     4.569930
C(work)[T.hos]     2.668831
dtype: float64

Out[39]:

(0.5953116925291129, 0.5526627461285702)

In [40]:

from ministats.plots.figures import plot_lm_anova

with plt.rc_context({"figure.figsize":(5,3), "text.usetex":True}):
    ax = plot_lm_anova(doctors, x="work", y="score")
    ax.set_ylim([31,69])    
    sns.move_legend(ax, "lower right")

from ministats.plots.figures import plot_lm_anova with plt.rc_context({"figure.figsize":(5,3), "text.usetex":True}): ax = plot_lm_anova(doctors, x="work", y="score") ax.set_ylim([31,69]) sns.move_legend(ax, "lower right")

In [41]:

# BONUS: print ANOVA table
# import statsmodels.api as sm
# sm.stats.anova_lm(lmw)

# BONUS: print ANOVA table # import statsmodels.api as sm # sm.stats.anova_lm(lmw)

Nonparametric tests¶

One-sample Wilcoxon signed-rank test¶

In [42]:

kombucha = pd.read_csv("../datasets/kombucha.csv")
ksample04 = kombucha[kombucha["batch"]==4]["volume"]

# Zero-centered volumes
zcksample04 = ksample04 - 1000

from scipy.stats import wilcoxon
reswil = wilcoxon(zcksample04)
reswil.pvalue

kombucha = pd.read_csv("../datasets/kombucha.csv") ksample04 = kombucha[kombucha["batch"]==4]["volume"] # Zero-centered volumes zcksample04 = ksample04 - 1000 from scipy.stats import wilcoxon reswil = wilcoxon(zcksample04) reswil.pvalue

Out[42]:

0.002770629538645153

In [43]:

# Create a new data frame with the signed ranks of the volumes
df_zcsr = pd.DataFrame()
df_zcsr["zcvolume_sr"] = np.sign(zcksample04) * zcksample04.abs().rank()

lmwil = smf.ols("zcvolume_sr ~ 1", data=df_zcsr).fit()
lmwil.pvalues.iloc[0]

# Create a new data frame with the signed ranks of the volumes df_zcsr = pd.DataFrame() df_zcsr["zcvolume_sr"] = np.sign(zcksample04) * zcksample04.abs().rank() lmwil = smf.ols("zcvolume_sr ~ 1", data=df_zcsr).fit() lmwil.pvalues.iloc[0]

Out[43]:

0.0022841508459744237

Mann-Whitney U-test¶

In [44]:

scoresR = doctors[doctors["loc"]=="rur"]["score"]
scoresU = doctors[doctors["loc"]=="urb"]["score"]

from scipy.stats import mannwhitneyu
resmwu = mannwhitneyu(scoresU, scoresR)
resmwu.pvalue

scoresR = doctors[doctors["loc"]=="rur"]["score"] scoresU = doctors[doctors["loc"]=="urb"]["score"] from scipy.stats import mannwhitneyu resmwu = mannwhitneyu(scoresU, scoresR) resmwu.pvalue

Out[44]:

0.050083369850737636

In [45]:

# Compute the (unsigned) ranks of the scores
doctors["score_r"] = doctors["score"].rank()

# Fit a linear model
lmmwu = smf.ols("score_r ~ 1 + C(loc)", data=doctors).fit()
lmmwu.pvalues.iloc[1]

# Compute the (unsigned) ranks of the scores doctors["score_r"] = doctors["score"].rank() # Fit a linear model lmmwu = smf.ols("score_r ~ 1 + C(loc)", data=doctors).fit() lmmwu.pvalues.iloc[1]

Out[45]:

0.049533887469988734

Kruskal-Wallis analysis of variance by ranks¶

In [46]:

from scipy.stats import kruskal
reskw = kruskal(scoresH, scoresC, scoresE)
reskw.pvalue

from scipy.stats import kruskal reskw = kruskal(scoresH, scoresC, scoresE) reskw.pvalue

Out[46]:

0.4441051932875236

In [47]:

# Compute the (unsigned) ranks of the scores
doctors["score_r"] = doctors["score"].rank()  

lmkw = smf.ols("score_r ~ 1 + C(work)", data=doctors).fit()
lmkw.f_pvalue

# Compute the (unsigned) ranks of the scores doctors["score_r"] = doctors["score"].rank() lmkw = smf.ols("score_r ~ 1 + C(work)", data=doctors).fit() lmkw.f_pvalue

Out[47]:

0.44688872149660885

Explanations¶

In [ ]:

Dummy coding options¶

In [48]:

dmatrix("cat", data=catdf)

dmatrix("cat", data=catdf)

Out[48]:

DesignMatrix with shape (4, 3)
  Intercept  cat[T.B]  cat[T.C]
          1         0         0
          1         1         0
          1         0         1
          1         0         1
  Terms:
    'Intercept' (column 0)
    'cat' (columns 1:3)

In [49]:

dmatrix("C(cat)", data=catdf)

dmatrix("C(cat)", data=catdf)

Out[49]:

DesignMatrix with shape (4, 3)
  Intercept  C(cat)[T.B]  C(cat)[T.C]
          1            0            0
          1            1            0
          1            0            1
          1            0            1
  Terms:
    'Intercept' (column 0)
    'C(cat)' (columns 1:3)

In [50]:

dmatrix("C(cat, Treatment)", data=catdf)

dmatrix("C(cat, Treatment)", data=catdf)

Out[50]:

DesignMatrix with shape (4, 3)
  Intercept  C(cat, Treatment)[T.B]  C(cat, Treatment)[T.C]
          1                       0                       0
          1                       1                       0
          1                       0                       1
          1                       0                       1
  Terms:
    'Intercept' (column 0)
    'C(cat, Treatment)' (columns 1:3)

In [51]:

dmatrix("C(cat, Treatment('B'))", data=catdf)
# ALT. dmatrix("C(cat, Treatment(1))", data=catdf)

dmatrix("C(cat, Treatment('B'))", data=catdf) # ALT. dmatrix("C(cat, Treatment(1))", data=catdf)

Out[51]:

DesignMatrix with shape (4, 3)
  Intercept  C(cat, Treatment('B'))[T.A]  C(cat, Treatment('B'))[T.C]
          1                            1                            0
          1                            0                            0
          1                            0                            1
          1                            0                            1
  Terms:
    'Intercept' (column 0)
    "C(cat, Treatment('B'))" (columns 1:3)

Avoiding perfect collinearity¶

In [52]:

df_col = pd.DataFrame()
df_col["iscli"] = (doctors["work"] == "cli").astype(int)
df_col["iseld"] = (doctors["work"] == "eld").astype(int)
df_col["ishos"] = (doctors["work"] == "hos").astype(int)
df_col["score"] = doctors["score"]

df_col = pd.DataFrame() df_col["iscli"] = (doctors["work"] == "cli").astype(int) df_col["iseld"] = (doctors["work"] == "eld").astype(int) df_col["ishos"] = (doctors["work"] == "hos").astype(int) df_col["score"] = doctors["score"]

In [53]:

formula_col = "score ~ 1 + iscli + iseld + ishos"
lm_col = smf.ols(formula_col, data=df_col).fit()
lm_col.params

formula_col = "score ~ 1 + iscli + iseld + ishos" lm_col = smf.ols(formula_col, data=df_col).fit() lm_col.params

Out[53]:

Intercept    36.718781
iscli         9.826673
iseld        14.396603
ishos        12.495504
dtype: float64

In [54]:

lm_col.condition_number

lm_col.condition_number

Out[54]:

4594083276761821.0

In [55]:

lm2.params

lm2.params

Out[55]:

Intercept    60.452901
alc          -1.800101
weed         -1.021552
exrc          1.768289
dtype: float64

Discussion¶

Other coding strategies for categorical variables¶

In [56]:

dmatrix("0 + C(cat)", data=catdf)

dmatrix("0 + C(cat)", data=catdf)

Out[56]:

DesignMatrix with shape (4, 3)
  C(cat)[A]  C(cat)[B]  C(cat)[C]
          1          0          0
          0          1          0
          0          0          1
          0          0          1
  Terms:
    'C(cat)' (columns 0:3)

In [57]:

dmatrix("1 + C(cat, Sum)", data=catdf)

dmatrix("1 + C(cat, Sum)", data=catdf)

Out[57]:

DesignMatrix with shape (4, 3)
  Intercept  C(cat, Sum)[S.A]  C(cat, Sum)[S.B]
          1                 1                 0
          1                 0                 1
          1                -1                -1
          1                -1                -1
  Terms:
    'Intercept' (column 0)
    'C(cat, Sum)' (columns 1:3)

In [58]:

dmatrix("1+C(cat, Diff)", data=catdf)

dmatrix("1+C(cat, Diff)", data=catdf)

Out[58]:

DesignMatrix with shape (4, 3)
  Intercept  C(cat, Diff)[D.A]  C(cat, Diff)[D.B]
          1           -0.66667           -0.33333
          1            0.33333           -0.33333
          1            0.33333            0.66667
          1            0.33333            0.66667
  Terms:
    'Intercept' (column 0)
    'C(cat, Diff)' (columns 1:3)

In [59]:

dmatrix("C(cat, Helmert)", data=catdf)

dmatrix("C(cat, Helmert)", data=catdf)

Out[59]:

DesignMatrix with shape (4, 3)
  Intercept  C(cat, Helmert)[H.B]  C(cat, Helmert)[H.C]
          1                    -1                    -1
          1                     1                    -1
          1                     0                     2
          1                     0                     2
  Terms:
    'Intercept' (column 0)
    'C(cat, Helmert)' (columns 1:3)

Exercises¶

EXX: redo comparison of debate and lectures scores¶

In [60]:

students = pd.read_csv("../datasets/students.csv")
lmcu = smf.ols("score ~ 1 + C(curriculum)", data=students).fit()
lmcu.tvalues.iloc[1], lmcu.pvalues.iloc[1]

students = pd.read_csv("../datasets/students.csv") lmcu = smf.ols("score ~ 1 + C(curriculum)", data=students).fit() lmcu.tvalues.iloc[1], lmcu.pvalues.iloc[1]

Out[60]:

(-1.7197867420465656, 0.10917234443214403)

EXX: model comparison¶

In [61]:

formula3w = "score ~ 1 + alc + weed + exrc + C(loc) + C(work)"
lm3w = smf.ols(formula3w, data=doctors).fit()

formula3 = "score ~ 1 + alc + weed + exrc + C(loc)"
lm3 = smf.ols(formula3, data=doctors).fit()

lm3w.compare_f_test(lm3)

formula3w = "score ~ 1 + alc + weed + exrc + C(loc) + C(work)" lm3w = smf.ols(formula3w, data=doctors).fit() formula3 = "score ~ 1 + alc + weed + exrc + C(loc)" lm3 = smf.ols(formula3, data=doctors).fit() lm3w.compare_f_test(lm3)

Out[61]:

(1.5158185269522577, 0.22299549360241236, 2.0)

The result is non-significant which means including the predictor C(work) in the model is not useful.

EXX: run ANOVA test¶

In [62]:

# Construct data as a pd.DataFrame
np.random.seed(42)
As = np.random.normal(0, 1, 20)
Bs = np.random.normal(-2, 1, 20)
Cs = np.random.normal(3, 1, 20)
Ds = np.random.normal(1.5, 1, 20)

dfABCD = pd.DataFrame()
dfABCD["group"] = ["A"]*20 + ["B"]*20 + ["C"]*20 + ["D"]*20
dfABCD["value"] = np.concatenate([As, Bs, Cs, Ds])

with plt.rc_context({"figure.figsize":(8,6), "text.usetex":True}):
    ax = plot_lm_anova(dfABCD, x="group", y="value")

from scipy.stats import f_oneway
resABCD = f_oneway(As, Bs, Cs, Ds)
print(resABCD.statistic, resABCD.pvalue)

lmabcd =  smf.ols("value ~ C(group)", data=dfABCD).fit()
lmabcd.fvalue, lmabcd.f_pvalue

# Construct data as a pd.DataFrame np.random.seed(42) As = np.random.normal(0, 1, 20) Bs = np.random.normal(-2, 1, 20) Cs = np.random.normal(3, 1, 20) Ds = np.random.normal(1.5, 1, 20) dfABCD = pd.DataFrame() dfABCD["group"] = ["A"]*20 + ["B"]*20 + ["C"]*20 + ["D"]*20 dfABCD["value"] = np.concatenate([As, Bs, Cs, Ds]) with plt.rc_context({"figure.figsize":(8,6), "text.usetex":True}): ax = plot_lm_anova(dfABCD, x="group", y="value") from scipy.stats import f_oneway resABCD = f_oneway(As, Bs, Cs, Ds) print(resABCD.statistic, resABCD.pvalue) lmabcd = smf.ols("value ~ C(group)", data=dfABCD).fit() lmabcd.fvalue, lmabcd.f_pvalue

107.22963883851017 3.091116115443299e-27

Out[62]:

(107.22963883851006, 3.091116115443401e-27)

Links¶

• Patsy and Statsmodels https://www.youtube.com/watch?v=iEANEcWqAx4
• Tests as LMs: https://lindeloev.github.io/tests-as-linear/
• https://stats.stackexchange.com/questions/59047/how-are-regression-the-t-test-and-the-anova-all-versions-of-the-general-linear
• https://danielroelfs.com/blog/everything-is-a-linear-model/ via HN